¿Qué es la Unidad Interactiva de Matemáticas para Sexto Grado de Primaria?

La Unidad Interactiva de Matemáticas para Sexto Grado, es una iniciativa del Proyecto Prometeo, quien ha sostenido su vigencia durante casi una década, manteniéndose al margen de ideologías y de publicidad, con el afán de consolidarse como una herramienta de apoyo a la educación de todos los niveles educativos. He sostenido que los estudiantes del siglo XXI, son nativos tecnológicos y que la educación debe asumir este nuevo reto. Sumado a lo anterior el nuevo escenario planteado por la pandemia ha obligado a los sistemas educativos recurrir ineludiblemente a la tecnología como su única forma de activar procesos de enseñanza en todo el mundo.

Es importante destacar mi agradecimiento al Proyecto Descartes, quien ha facilitado los códigos necesarios para la realización de esta obra que no tiene otro propósito que de fortalecer la educación que en este caso específico se refiere a la asignatura de Matemáticas en sexto grado de primaria.

Profr. Víctor Manuel Navarro

Título de la obra:
UNIDAD INTERACTIVA DE MATEMÁTICAS PARA SEXTO GRADO

Autor:
PROFR. VICTOR MANUEL NAVARRO

Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono

DESCARGA DE LA EDICIÓN

LICENCIA

El contendido de esta obra esta bajo una licencia Creative Commons (Atribución-NoComercial-CompartirIgual).

Tabla de contenido

Prefacio

El propósito de esta unidad interactiva de Matemáticas para sexto grado es brindar una oportinidad de aprendizaje a los estudiantes que en este instante experimentan el confinamiento y que sus posibilidades se han reducido al uso sistemático de la tecnología como la única herramienta capaz de solventar las actuales necesidades educativas.

Para la realización de la presente herramienta he sustraído los aprendizajes clave anidados en los campos de formación académica y en específico del pensamiento matemático y de sus tres principales ejes bajo los cuales se conforman los temas que generan los aprendizajes esperados.

El Proyecto Prometeo, ha sido desde tiempos un proveedor de insumos previamente curados y alineados a las necesidades de los aprendizajes del plan de estudio que han facilitado a los padres de familia, estudiantes y docentes su apropiación.

Con esta nueva aportación Prometeo, rescata los aprendizajes clave del programa 2017 y enlaza recursos propios que habrán de facilitar su estudio y reflexión de los diferentes temas. Ante lo cual Prometeo rebasa una nueva frontera de actualización.

Resuelve problemas de multiplicación con fracciones y decimales, con multiplicador número natural, y de división con cociente o divisores naturales.

Analiza y explora el siguiente material

Cuando se trata de problemas en los que se involucra la distribución de cantidades, la división es la herramienta ideal. Esto también aplica cuando las cantidades comprometidas son fracciones

En esta ocasión se deben distribuir diez litros de agua en partes de 2/3 de litro cada una. Es decir, se está preguntando cuántas veces está 2/3 en diez. Para responder esta pregunta se debe hacer la división:
10 ÷ 2/3.
Recuerda que para poder operar los enteros con fraccionarios, se debe poner un uno como denominador, en este caso 10= 10/1 .
En la siguiente imagen puedes ver el procedimiento completo para realizar esta división:

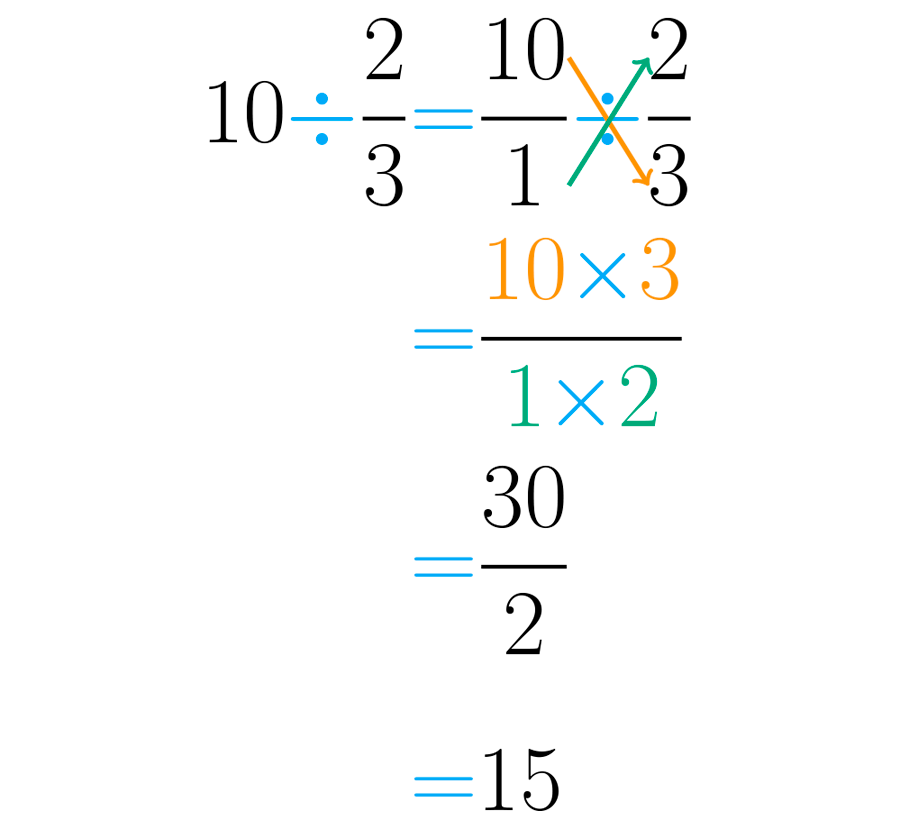
La división es la operación inversa de la multiplicación. Conocido el producto de dos números y uno de los factores, dividir es hallar el otro factor, es hallar el número por el que debo multiplicar al factor conocido para obtener el producto dado

Lee, escribe y ordena números naturales de cualquier cantidad de cifras, fracciones y números decimales.

Estima e interpreta números en el sistema de numeración maya.

Lee y escribe números romanos.

Resuelve problemas que impliquen el uso de números enteros al situarlos en la recta numérica, compararlos y ordenarlos.

Resuelve problemas de suma y resta con números naturales, decimales y fracciones.

Usa el algoritmo convencional para sumar y restar decimales.

Calcula mentalmente, de manera exacta y aproximada, sumas y restas de decimales.

Compara razones expresadas mediante dos números naturales (n por cada m) y con una fracción (n/m).

Calcula valores faltantes en problemas de proporcionalidad directa, con un número natural como constante.

Resuelve problemas de cálculo de porcentajes y de tanto por ciento.

Calcula mentalmente porcentajes (50%, 25%, 10% y 1%) que sirvan de base para cálculos más complejos.

Analiza sucesiones de números y de figuras con progresión aritmética y geométrica.

Toda secuencia ordenada de números reales recibe el nombre de sucesión. Dentro del grupo de sucesiones existen dos particularmente interesantes por el principio de regularidad que permite sistematizar la definición de sus propiedades: las progresiones aritméticas y geométricas.

Una sucesión es un conjunto de cosas (normalmente números) en un cierto orden.

Lee, interpreta y diseña planos y mapas para comunicar oralmente o por escrito la ubicación de seres, objetos y trayectos.

Resuelve situaciones que impliquen la ubicación de puntos en el plano cartesiano.

¿Como graficar figuras en el plano cartesiano? Para saber ubicar puntos en el plano cartesiano y formar figuras utilizando el concepto del plano cartesiano estudiando en primaria, utilizamos un programa que nos permite graficarlos. Localizamos puntos formados por pares ordenados de números o coordenadas cartesianas para crear figuras.

Se conoce como plano cartesiano, coordenadas cartesianas o sistema cartesiano, a dos rectas numéricas perpendiculares, una horizontal y otra vertical, que se cortan en un punto llamado origen o punto cero. La finalidad del plano cartesiano es describir la posición o ubicación de un punto en el plano, la cual está representada por el sistema de coordenadas. El plano cartesiano también sirve para analizar matemáticamente figuras geométricas como la parábola, la hipérbole, la línea, la circunferencia y la elipse, las cuales forman parte de la geometría analítica.

Construye triángulos con regla y compás, traza e identifica sus alturas.

Construye prismas y pirámides rectos cuya base sea un rectángulo o un triángulo a partir de su desarrollo plano.

Calcula y compara el área de triángulos y cuadriláteros mediante su transformación en un rectángulo.

Estima, compara y ordena el volumen de prismas rectos rectangulares mediante el conteo de cubos.

Lee gráficas circulares.

Un gráfico circular es una manera visual de mostrar la información que se escribe en porcentajes. El círculo de un gráfico circular representa el 100%. Las partes de un entero que representan los objetos que se grafican se muestran en forma de cuñas. Cada cuña muestra qué parte del 100 representa el objeto.

Usa e interpreta la moda, la media aritmética y el rango de un conjunto de datos.

Para resumir un conjunto de datos numéricos podemos utilizar la media aritmética, la mediana o la moda. La media aritmética o promedio representa el reparto equitativo, el equilibrio, la equidad. Es el valor que tendrían los datos, si todos ellos fueran iguales. O, también, el valor que correspondería a cada uno de los datos de la distribución si su suma total se repartiera por igual. Si se ordenan todos los datos, de menor a mayor, la mediana es el valor que ocupa la posición central. Si el número de datos es par, la mediana es la media aritmética de los dos centrales. La moda es el valor que más se repite o, lo que es lo mismo, el que tiene la mayor frecuencia

Determina los resultados posibles de un experimento aleatorio.

ESPACIO MUESTRAL (S) De un experimento aleatorio, es el conjunto de todos los posibles resultados al realizar el experimento